C++ and Computer Architecture#
C++ is the programming language chosen for implementing numerical methods because it runs fast. C++ has one of the most advanced compilers. The compiler is able to generate fast machine code. C++ also allows to directly write fast assembly.
The second is maintenance. A numerical system usually takes years to develop. When proven useful, it will be maintained for decades. Such a long-living system needs extensive support from the compiler. C++ offers it. The stable interface makes it possible to access a wide range of third-party software.
C++ is hard and it is impossible to cover it from end to end. In this chapter we will make a basic introduction with Compile and Link, C++ Integer Types, Pointer and Array Indexing, and Floating-Point Value. Then we will discuss Object-Oriented Programming, which is critically important for a system achieving speed and flexibility in the same time. After that, we will cover the productive skills of Standard Template Library (STL), Polymorphism, and Curiously Recursive Template Pattern (CRTP).
Compile and Link#
Compiler is a complex system. The most common way to use it is to execute the
compiler driver from the command-line. For example, of GCC, the C++ compiler
driver is g++. It accepts a lot of command-line arguments. The simplest
for is to supply an input and an output.
Before run the compiler, assume the program file is:
helloworld.cpp)#1 2 3 4 5 6 | #include <iostream>
int main(int argc, char ** argv)
{
std::cout << "hello, world" << std::endl;
return 0;
}
|
Run the compiler:
$ g++ helloworld.cpp -o helloworld
A binary named helloworld is produced by using the command-line argument
-o. The binary contains the executable code:
$ ./helloworld
hello, world
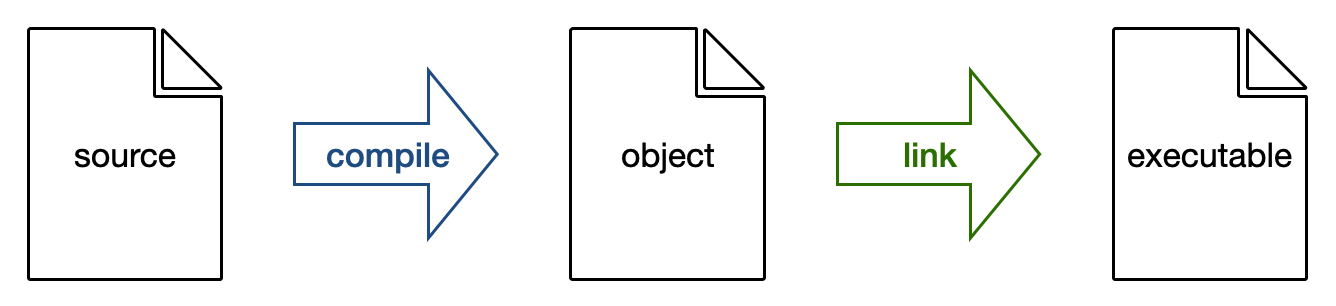
The g++ command does two things: compilation and then linking. When running the compiler with
the argument -c, it performs only the compiling part to take the source
code and output the object file. The object file contains the machine code,
but doesn’t include the functions not defined in the source file.
Useful tool: compiler explorer
When you want to test any code snippets or any command-line arguments in any compilers on any platforms, check the compiler explorer website: https://godbolt.org.
The argument -o is also used to specify the output object file name:
$ g++ -c helloworld.cpp -o helloworld.o
$ file helloworld.o
helloworld.o: Mach-O 64-bit object x86_64
Although an object file contains the compiled code, it may not be directly executed, because it is not linked yet:
$ chmod a+x helloworld.o
$ ./helloworld.o
-bash: ./helloworld.o: cannot execute binary file
$ file helloworld.o
helloworld.o: Mach-O 64-bit object x86_64
By dropping the -c argument, and supplying the object file as the input,
g++ will link the object file and necessary libraries into the executable:
$ g++ helloworld.o -o helloworld2
$ file helloworld2
helloworld: Mach-O 64-bit executable x86_64
$ ./helloworld2
hello, world
Separate Compilation Units#
In a larger project, it is common to separate the declaration of functions to
header files. The code implementing the functions is put in the so-called
implementation files. Usually a header file uses the extension name .h,
.hxx, or .hpp:
1 2 | #pragma once
void hello();
|
An implementation file uses .cc, .cxx, or .cpp:
1 2 3 4 5 6 | #include <iostream>
#include "hello.hpp"
void hello()
{
std::cout << "hello with standalone compiling unit" << std::endl;
}
|
Worker Code#
Because the main() function is not defined in hello.cpp, the file
cannot be built as a binary executable:
$ g++ hello.cpp -o hello
Undefined symbols for architecture x86_64:
"_main", referenced from:
implicit entry/start for main executable
ld: symbol(s) not found for architecture x86_64
clang: error: linker command failed with exit code 1 (use -v to see invocation)
We need to build the object file using -c.
$ g++ -c hello.cpp -o hello.o
Main Program#
The function main() is implemented in another file hellomain.cpp:
1 2 3 4 5 6 | #include "hello.hpp"
int main(int argc, char ** argv)
{
hello();
return 0;
}
|
If trying to build a binary executable solely with this file, we will receive a different linking error:
$ g++ hellomain.cpp -o hellomain.o
Undefined symbols for architecture x86_64:
"hello()", referenced from:
_main in hellomain-ce1e94.o
ld: symbol(s) not found for architecture x86_64
clang: error: linker command failed with exit code 1 (use -v to see invocation)
We should also build hellomain.cpp as an object file:
# hellomain.cpp also needs to be built as an object file
$ g++ -c hellomain.cpp -o hellomain.o
Link Object Files#
Now we have two object files and we can call g++ to link them to an
executable and run it:
$ g++ hello.o hellomain.o -o hellomain
$ ./hellomain
hello with standalone compiling unit
Include Syntax#
The directive #include may use two delimiters: "" or <>. The
former (see above) will search for the
include file in the current directory and then the system directories. The
latter will search only in the system directories:
1 2 3 4 5 6 | #include <hello.hpp>
int main(int argc, char ** argv)
{
hello();
return 0;
}
|
Since the current directory is not a system-search directory for the include file, the above file cannot be built with the same command line:
$ g++ -c hellomain.cpp -o hellomain.o
hellomain_sys.cpp:1:10: error: 'hello.hpp' file not found with <angled> include; use "quotes" instead
#include <hello.hpp>
^~~~~~~~~~~
"hello.hpp"
We need to tell the compiler frontend to search in the current directory by
using -I.:
$ g++ -I. -c hellomain.cpp -o hellomain.o
Make Static Library#
If we have multiple object files, they can be combined into a static library for linking later. The following example uses the only object file we have to show how to do it:
$ g++ -c hello.cpp -o hello.o
$ ar rcs libhello.a hello.o
To use the library file, tell g++ using -l followed by the library name
hello. The path to search for the library files should be supplied with
-L followed by the path.
$ g++ -c hellomain.cpp -o hellomain.o
$ g++ hellomain.o -L. -lhello -o hellomain2
$ ./hellomain2
hello with standalone compiling unit
Use Existing Library#
Usually we will use libraries that is prepared by someone else (third-party). In the following example, the code includes the header file (which is assumed to be in the header file search paths) for the BLAS library:
distance.cpp)#1 2 3 4 5 6 7 8 9 10 11 | #include <iostream>
#include <cblas.h>
int main(int, char **)
{
double vx[] = {1, 2};
double vy[] = {-2, 1};
std::cout << "x = (" << vx[0] << ", " << vx[1] << ")" << std::endl;
std::cout << "y = (" << vy[0] << ", " << vy[1] << ")" << std::endl;
std::cout << "x \\dot y = " << cblas_ddot(2, vx, 1, vy, 1) << std::endl;
return 0;
}
|
Although the compiler recognizes the functions declared in the header file
cblas.h, the linker does not see it in object file:
$ g++ distance.cpp -o distance
Undefined symbols for architecture x86_64:
"_cblas_ddot", referenced from:
_main in distance-903338.o
ld: symbol(s) not found for architecture x86_64
clang: error: linker command failed with exit code 1 (use -v to see invocation)
We need to tell the linker to link the library cblas (which is also assumed
to be in the library search paths):
$ g++ distance.cpp -o distance -lcblas
$ ./distance
x = (1, 2)
y = (-2, 1)
x \dot y = 0
Note
We are also responsible for making sure the header file and library file are reachable by the compiler and linker. The compiler shows error when not finding the header file:
$ g++ distance.cpp -o distance
distance.cpp:2:10: fatal error: 'cblas.h' file not found
#include <cblas.h>
^~~~~~~~~
1 error generated.
The linker error:
$ g++ distance.cpp -o distance -lcblas
ld: library not found for -lcblas
clang: error: linker command failed with exit code 1 (use -v to see invocation)
C++ Integer Types#
Basic Integer Types#
Width of the fundamental types is specified by the standard to assist writing portable code.
Type Name |
Width |
|
|---|---|---|
Boolean |
|
|
Signed integer |
|
at least 16 bits |
|
at least 16 bits |
|
|
at least 32 bits |
|
|
at least 64 bits |
|
Unsigned integer |
|
at least 16 bits |
|
at least 16 bits |
|
|
at least 32 bits |
|
|
at least 64 bits |
|
Character |
|
8 bits |
Unsigned character |
|
8 bits |
You can check the number of bytes of each of types using the example code types.cpp:
$ g++ types.cpp -o types
$ ./types
unit is byte
sizeof(char): 1
sizeof(short): 2
sizeof(int): 4
sizeof(long): 8
sizeof(long long): 8
sizeof(unsigned char): 1
sizeof(unsigned short): 2
sizeof(unsigned int): 4
sizeof(unsigned long): 8
sizeof(unsigned long long): 8
Fixed-Width Integer Types#
The C++ standard library provides the fixed-width (bit) integer types which are the same as C in the header file <cstdint>. Fixed width matters for numerical code more than hardware architecture does. It’s easier for numerical code to break by changed width of indexing integer than by changed addressing space.
Type Name |
Width |
|
|---|---|---|
Signed integer |
|
8 bits / 1 byte |
|
16 bits / 2 byte |
|
|
32 bits / 4 byte |
|
|
64 bits / 8 byte |
|
Unsigned integer |
|
8 bits / 1 byte |
|
16 bits / 2 byte |
|
|
32 bits / 4 byte |
|
|
64 bits / 8 byte |
You can check the number of bytes of each of types using the example code cstdint.cpp:
$ g++ cstdint.cpp -o cstdint
$ ./cstdint
unit is byte
sizeof(int8_t): 1
sizeof(uint8_t): 1
sizeof(int16_t): 2
sizeof(uint16_t): 2
sizeof(int32_t): 4
sizeof(uint32_t): 4
sizeof(int64_t): 8
sizeof(uint64_t): 8
Signness#
Care should be taken when signed and unsigned integers are both used in code. Comparison result between signed and unsigned integers is sometimes surprising. That’s see what it is with the example code:
signness.cpp)#1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream>
#include <cstdint>
int main(int, char **)
{
long sint = -1;
unsigned long uint = 1;
std::cout << "sint: " << sint << std::endl;
std::cout << "uint: " << uint << std::endl;
if (sint > uint)
{
std::cout << "sint > uint, although it can't be" << std::endl;
}
return 0;
}
|
It shows that the negative value is greater than the positive value:
$ g++ signness.cpp -o signness
$ ./signness
sint: -1
uint: 1
sint > uint, although it can't be
It’s such a common mistake that compiler provides a check:
$ g++ signness.cpp -o signness -Wsign-compare -Werror
signness.cpp:9:14: error: comparison of integers of different signs: 'long' and 'unsigned long' [-Werror,-Wsign-compare]
if (sint > uint) { std::cout << "sint > uint, although it can't be" << std::endl; }
~~~~ ^ ~~~~
1 error generated.
Note
The common wisdom advises to not mixing signed and unsigned integer, but in numerical code negative indices are commonplace. On the other hand, STL almost always uses unsigned integers for indexing. It is unavoidable to mix the signed and unsigned integer in some places. When we are forced to write it, make the reasons very clear in the code.
Pointer and Array Indexing#
Integers are used extensively in array indexing. It wouldn’t surprise anyone for they are the only thing that can be used to index elements in arrays. Here we use the example of “Index arrays using integers (arrays.cpp)” to explain how they are used. The code is built with:
$ g++ arrays.cpp -o arrays -Wall -Wextra -Werror
The code creates a conventional C-style array data. Two pointers
pdata and odata are created for the array.
// C-style POD array.
int32_t data[100];
// Make a pointer to the head address of the array.
int32_t * pdata = data;
// Make another pointer to the 50-th element from the head of the array.
int32_t * odata = pdata + 50;
// Initialize the array.
for (size_t it=0; it<100; ++it) { data[it] = it + 5000; }
Pointer as Array#
Both data “the array” and pdata “the pointer” work like
arrays when indexing. It is shown by printing the 10-th element of
data and pdata:
std::cout << "data[10]: " << data[10] << std::endl;
std::cout << "pdata[10]: " << pdata[10] << std::endl;
Both show the same element:
data[10]: 5010
pdata[10]: 5010
In the other way around, data works like a pointer:
std::cout << "*(data+20): " << *(data+20) << std::endl;
std::cout << "*(pdata+20): " << *(pdata+20) << std::endl;
data and pdata point to the same address, and the 20-th
offset element is the same:
*(data+20): 5020
*(pdata+20): 5020
Now look at the pointer that is already offset by 50 element, odata:
std::cout << "data[50]: " << data[50] << std::endl;
std::cout << "odata[0]: " << odata[0] << std::endl;
The two statements print the same element:
data[50]: 5050
odata[0]: 5050
Negative Index#
Now we show how negative index works:
std::cout << "data[40]: " << data[40] << std::endl;
std::cout << "odata[-10]: " << odata[-10] << std::endl;
Since odata points to the 50-th element of data, the
“-10”-th element of odata should be the 40-th of data:
data[40]: 5040
odata[-10]: 5040
The same can be done with pointer offset, which may look more reasonable although it works the same as array indexing:
std::cout << "*(data+40): " << *(data+40) << std::endl;
std::cout << "*(odata-10): " << *(odata-10) << std::endl;
The output:
*(data+40): 5040
*(odata-10): 5040
Note
Negative indices should only be used when we know they do not go out of
range. That is why in the above example we set odata by
offsetting data by 50 elements. Accessing memory out of range
may result in segmentation fault or corrupted memory. The former crashes the
process immediately and the latter leads to unpredictable behaviors, which is
much harder to debug than the former.
Floating-Point Value#
x86 architecture follows the IEEE 754-1985 standard for floating-point. A floating-point value uses 3 fields to represent: sign, exponent (biased) (denoted by \(p\)), and fraction (denoted by \(f\) and \(f<1\)). The formula is:
Note that the number is binary-based.
x86 follows IEEE 754 standard for floating-point. There are two commonly used
floating-point formats: single and double precision. The C++ type names are
float and double, respectively.
Single-Precision (float)#
Single-precision floating-point value uses 32 bits (4 bytes). The first 23
bits are fraction. The following 8 bits are exponent. The last (highest) bit
is sign; 0 is positive while 1 is negative. In C++, the type name is
float.
Conisder a decimal number 2.75, which we use as an example to show how to get the fields. Write it by using the base of 2:
The bit fields for its IEEE 754 single-precision floating-point are:
sign (1 bit) |
exponent (8 bits) |
fraction (23 bits) |
|---|---|---|
|
|
|
The exponent bias for single-precision floating-point is 127 (\((\mathtt{0111 \, 1111})_2\)).
The floating-point value is usually inexact. For example, 0.3, although it
is rational, cannot be exactly represented as a single-precision
floating-point. Because the single-precision is 2-based, you should not follow
the arithmetic intuition learned from the 10-based number system.
float#1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | #include <iostream>
#include <iomanip>
#include <bitset>
#include <cstdint>
int main(int, char **)
{
float fvalue;
std::bitset<32> b32value;
fvalue = 0.3;
b32value = *reinterpret_cast<uint32_t *>(&fvalue);
std::cout << "fvalue: " << std::setprecision(10) << fvalue << std::endl;
std::cout << "b32value (float sep): ";
std::cout << " "; for (size_t it=0; it<1; ++it) { std::cout << b32value[31-it]; }
std::cout << " "; for (size_t it=1; it<9; ++it) { std::cout << b32value[31-it]; }
std::cout << " "; for (size_t it=9; it<32; ++it) { std::cout << b32value[31-it]; }
std::cout << std::endl;
std::cout << " sign exponent fraction" << std::endl;
fvalue = 3;
b32value = *reinterpret_cast<uint32_t *>(&fvalue);
std::cout << "fvalue: " << std::setprecision(10) << fvalue << std::endl;
std::cout << "b32value (float sep): ";
std::cout << " "; for (size_t it=0; it<1; ++it) { std::cout << b32value[31-it]; }
std::cout << " "; for (size_t it=1; it<9; ++it) { std::cout << b32value[31-it]; }
std::cout << " "; for (size_t it=9; it<32; ++it) { std::cout << b32value[31-it]; }
std::cout << std::endl;
std::cout << " sign exponent fraction" << std::endl;
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 | $ g++ float.cpp -o float
$ ./float
fvalue: 0.3000000119
b32value (float sep): 0 01111101 00110011001100110011010
sign exponent fraction
fvalue: 3
b32value (float sep): 0 10000000 10000000000000000000000
sign exponent fraction
|
Double-Precision (double)#
Double-precision floating-point value uses 64 bits (8 bytes). The first 52
bits are fraction. The following 11 bits are exponent. The last (highest) bit
is sign; 0 is positive while 1 is negative. In C++, the type name is double.
Use the same example of 2.75 for the double-precision floating-point. Write \(2.75 = (1.011)_2 \times 2^1\). The exponent bias for double-precision floating-point is 1023 (\((\mathtt{011 \, 1111 \, 1111})_2\)). The bit fields are:
sign (1 bit) |
exponent (11 bits) |
fraction (52 bits) |
|---|---|---|
|
|
|
Compared with the single-precision version:
sign (1 bit) |
exponent (8 bits) |
fraction (23 bits) |
|---|---|---|
|
|
|
Numeric Limits#
Both C and C++ provides constants for the value limit of each type. In C++,
the constants are available through include file limits.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | #include <iostream>
#include <cstdint>
#include <limits>
int main(int, char **)
{
std::cout << "type\t\tlowest()\tmin()\t\tmax()\t\tepsilon()" << std::endl << std::endl;
std::cout << "float\t\t"
<< std::numeric_limits<float>::lowest() << "\t"
<< std::numeric_limits<float>::min() << "\t"
<< std::numeric_limits<float>::max() << "\t"
<< std::numeric_limits<float>::epsilon() << "\t"
<< std::endl;
std::cout << "double\t\t"
<< std::numeric_limits<double>::lowest() << "\t"
<< std::numeric_limits<double>::min() << "\t"
<< std::numeric_limits<double>::max() << "\t"
<< std::numeric_limits<double>::epsilon() << "\t"
<< std::endl;
std::cout << "int32_t\t\t"
<< std::numeric_limits<int32_t>::lowest() << "\t"
<< std::numeric_limits<int32_t>::min() << "\t"
<< std::numeric_limits<int32_t>::max() << "\t"
<< std::numeric_limits<int32_t>::epsilon() << "\t"
<< std::endl;
std::cout << "uint32_t\t"
<< std::numeric_limits<uint32_t>::lowest() << "\t\t"
<< std::numeric_limits<uint32_t>::min() << "\t\t"
<< std::numeric_limits<uint32_t>::max() << "\t"
<< std::numeric_limits<uint32_t>::epsilon() << "\t"
<< std::endl;
std::cout << "int64_t\t\t"
<< std::numeric_limits<int64_t>::lowest() << "\t"
<< std::numeric_limits<int64_t>::min() << "\t"
<< std::numeric_limits<int64_t>::max() << "\t"
<< std::numeric_limits<int64_t>::epsilon() << "\t"
<< std::endl;
std::cout << "uint64_t\t"
<< std::numeric_limits<uint64_t>::lowest() << "\t\t"
<< std::numeric_limits<uint64_t>::min() << "\t\t"
<< std::numeric_limits<uint64_t>::max() << "\t"
<< std::numeric_limits<uint64_t>::epsilon() << "\t"
<< std::endl;
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 9 10 | $ g++ nlimits.cpp -o nlimits
$ ./nlimits
type lowest() min() max() epsilon()
float -3.40282e+38 1.17549e-38 3.40282e+38 1.19209e-07
double -1.79769e+308 2.22507e-308 1.79769e+308 2.22045e-16
int32_t -2147483648 -2147483648 2147483647 0
uint32_t 0 0 4294967295 0
int64_t -9223372036854775808 -9223372036854775808 9223372036854775807 0
uint64_t 0 0 18446744073709551615 0
|
Exception Handling#
The pragma “#pragma STDC FENV_ACCESS ON” turns on floating-point exception
handling in CPU. C++ defines the following floating-point exception that is
supported by the hardware:
macro |
math error condition |
description |
|---|---|---|
|
pole error |
math result was infinite or undefined |
|
inexact result |
rounding was required for the operation |
|
domain error |
the argument was outside the domain in which the math operation |
|
range error |
the result was too large to be representable |
|
range error |
the result became subnormal due to loss of precision |
|
n/a |
bitwise OR of all supported floating-point exceptions |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | #include <iostream>
#include <cfenv>
#include <cmath>
#include <limits>
int main(int, char **)
{
float v1;
feclearexcept(FE_ALL_EXCEPT);
v1 = 0.3;
std::cout << "result: " << v1/0 << std::endl;
if (fetestexcept(FE_DIVBYZERO)) { std::cout << " FE_DIVBYZERO" << std::endl; }
feclearexcept(FE_ALL_EXCEPT);
v1 = 2;
std::cout << "std::sqrt(2): " << std::sqrt(v1) << std::endl;
if (fetestexcept(FE_INEXACT)) { std::cout << " FE_INEXACT" << std::endl; }
feclearexcept(FE_ALL_EXCEPT);
v1 = 2;
std::cout << "std::acos(2): " << std::acos(v1) << std::endl;
if (fetestexcept(FE_INVALID)) { std::cout << " FE_INVALID" << std::endl; }
feclearexcept(FE_ALL_EXCEPT);
v1 = std::numeric_limits<float>::max();
std::cout << "std::numeric_limits<float>::max() * 2: " << v1 * 2 << std::endl;
if (fetestexcept(FE_OVERFLOW)) { std::cout << " FE_OVERFLOW" << std::endl; }
feclearexcept(FE_ALL_EXCEPT);
v1 = std::numeric_limits<float>::min();
std::cout << "std::numeric_limits<float>::min() / 10: " << v1 / 10 << std::endl;
if (fetestexcept(FE_UNDERFLOW)) { std::cout << " FE_UNDERFLOW" << std::endl; }
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 9 10 11 12 | $ g++ fpexc.cpp -o fpexc
$ ./fpexc
result: inf
FE_DIVBYZERO
std::sqrt(2): 1.41421
FE_INEXACT
std::acos(2): nan
FE_INVALID
std::numeric_limits<float>::max() * 2: inf
FE_OVERFLOW
std::numeric_limits<float>::min() / 10: 1.17549e-39
FE_UNDERFLOW
|
Object-Oriented Programming#
Object-oriented programming (OOP) allows us to organize data with logic. The organized entities are called objects. The point of using OOP is to make it easier to process the data. It usually may result in fewer lines of code and make more helper functions memorable. Because numerical software needs to process a lot of data, OOP becomes a natural design.
When writing OOP code, we should keep the SOLID principles in mind:
Single responsibility: Each class has one and only one responsibility.
Open-closed: Open for extension but closed for modification.
Liskov substitution: Reference to a base class can be replaced by a derived class without special code.
Interface segregation: Multiple smaller, client-specific interfaces work better than single bigger, general interface.
Dependency inversion: Depend on abstraction rather than concrete implementation.
Encapsulation#
Encapsulation is a central concept of OOP. C++ uses classes as a basic construct for encapsulation, i.e., separating the interface from the implementation detail. Consumers of the class should not know how the class is implemented internally.
C++ class uses 3 access controls to realize encapsulation:
The
privateaccess means only the class itself may access the member (data or functions).The
publicaccess means everything can access the member.The
protectedapplies to inherited classes. Only the defining class and its derived classes can accessprotected.
For private member data, we want a convention to distinguish them from other
variables. Prefixing m_ is a common one. Other popular choices include
mMember (prefixing m with camel-case) and member_ (postfixing
_).
Encapsulation is very useful for numerical code. In the first impression, the access control prevents “straight-forward” code to access data. However, when we start development it’s impossible to foresee all the logic and constructs. Without proper encapsulation, we may not productively move forward.
Class & Accessors#
C++ provides two keywords to define a class: class and struct.
In most cases one can be used to replace the other. By default, the
accessibility of class is private, if no access specifier is used.
class to declare a point class#1 2 3 4 5 6 7 8 9 10 | class PointClass
{
float m_x, m_y; // by default private.
public:
// Accessors
float getX() const { return m_x; }
float getY() const { return m_y; }
void setX(float v) { m_x = v; }
void setY(float v) { m_y = v; }
}; /* end class PointClass */
|
On the other hand, struct‘s default accessibility is public.
struct to declare a point class#1 2 3 4 | struct PointStruct
{
float m_x, m_y; // by default public.
}; /* end class PointStruct */
|
The full example code can be found in class.cpp.
In addition to the mostly equivalent behavior, conventionally, struct has a
strong implication that the type is a POD (plain old data). As such, when you
need a class, prefer class over struct. If you want a POD, use
struct.
To access the private member data, accessors are usually needed. It may be argued that in a good OO design, classes should not let their consumers know about its member data. But it is impractical to eliminate data classes from numerical code. If you cannot totally hide it from outside, accessors must be provided.
There are two major styles for accessors: get/set and one-method-name. The second style uses a reference to directly access member data.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | #include <iostream>
class PointClass
{
float m_x, m_y;
public:
// Accessors: get/set style.
float getX() const { return m_x; }
float getY() const { return m_y; }
void setX(float v) { m_x = v; }
void setY(float v) { m_y = v; }
// Accessors of alternate style: single method name.
float const & x() const { return m_x; } // getter
float & x() { return m_x; } // setter
float const & y() const { return m_y; } // getter
float & y() { return m_y; } // setter
}; /* end class PointClass */
int main(int, char **)
{
PointClass pntc;
pntc.setX(2); pntc.setY(4);
std::cout << "pntc.getX() = " << pntc.getX() << ", pntc.getY() = " << pntc.getY() << std::endl;
pntc.x() = 12; pntc.y() = 24;
std::cout << "pntc.x() = " << pntc.x() << ", pntc.y() = " << pntc.y() << std::endl;
return 0;
}
|
Execution results:
1 2 3 4 | $ g++ accessor.cpp -o accessor --std=c++11
$ ./accessor
pntc.getX() = 2, pntc.getY() = 4
pntc.x() = 12, pntc.y() = 24
|
Reference#
Reference is an important construct in C++ and used everywhere.
Like a pointer, a C++ reference allow aliasing. But unlike a pointer, a reference cannot be constructed without initialization, and is safer than a pointer.
1 2 3 4 5 6 7 8 9 10 11 | int v = 10;
std::cout << "v = " << v << std::endl;
int * pv; // pointer; danger: uninitialized
pv = &v;
*pv = 11;
std::cout << "v = " << v << std::endl;
int & rv = v; // reference
rv = 12;
std::cout << "v = " << v << std::endl;
// error: declaration of reference variable 'nrv' requires an initializer
//int & nrv;
|
A const reference is often used to alias a read-only object.
1 2 3 | int const & crv = v; // const reference
// error: cannot assign to variable 'crv' with const-qualified type 'const int &'
//crv = 12;
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #include <iostream>
int main(int, char **)
{
int v = 10;
std::cout << "v = " << v << std::endl;
int * pv; // pointer; danger: uninitialized
pv = &v;
*pv = 11;
std::cout << "v = " << v << std::endl;
int & rv = v; // reference
rv = 12;
std::cout << "v = " << v << std::endl;
// error: declaration of reference variable 'nrv' requires an initializer
//int & nrv;
int const & crv = v; // const reference
// error: cannot assign to variable 'crv' with const-qualified type 'const int &'
//crv = 12;
std::cout << "&v, pv, &rv, &crv (address): " << std::endl
<< " " << &v << std::endl
<< " " << pv << std::endl
<< " " << &rv << std::endl
<< " " << &crv << std::endl;
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 9 10 | $ g++ reference.cpp -o reference --std=c++11
$ ./reference
v = 10
v = 11
v = 12
&v, pv, &rv, &crv (address):
0x7ffee458314c
0x7ffee458314c
0x7ffee458314c
0x7ffee458314c
|
Constructor and Destructor#
A constructor of a class is called when an object of the class is instantiated (the object can also be called an instance). You may have as many constructors as you like. There are special constructors that the compiler provides even if you don’t. The most essential one is the default constructor. It does not have any argument, and is called when you declare a variable of the class.
1 2 3 4 5 | class Line // assume it possesses heavy resources
{
public:
Line(); // default constructor.
};
|
The other two special constructors are copy constructor and move constructor.
1 2 | Line & Line(Line const & ); // copy constructor
Line & Line(Line &&); // move constructor
|
A copy constructor is called when the compiler needs to copy the object:
1 2 | Line line1; // invokes default constructor
Line line2(line1); // invokes copy constructor
|
A move constructor is called when the compiler knows the object to be instantiated will move the resources from the argument:
1 | Line line3(std::move(line2)); // invokes move constructor
|
(Move semantics will be discussed in later lectures. See Move Semantics and Copy Elision.)
When an object is no longer in use, the compiler calls its destructor to remove it from memory. The destructor is responsible for releasing the resources that it no longer needs. (Failure to release the unused resource is called resource leak.)
1 2 3 4 5 6 7 8 9 10 | class Line
{
public:
Line(size_t size) : m_size(size), m_coord(new float[size*2]) {}
// Destructor.
~Line() { if (nullptr != m_coord) { delete[] m_coord; } }
private:
size_t m_size = 0; // number of points.
float * m_coord = nullptr; // memory buffer for the points.
};
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 | #include <cstdint>
#include <algorithm>
#include <utility>
#include <iostream>
class Line
{
public:
// Basic constructors.
Line() = default; // default constructor.
Line(Line const & ); // copy constructor.
Line(Line &&); // move constructor.
Line & operator=(Line const & ); // copy assignment operator.
Line & operator=(Line &&); // move assignment operator.
// Custom constructor.
Line(size_t size) : m_size(size), m_coord(new float[size*2]) {}
// Desctructor.
~Line() { if (nullptr != m_coord) { delete[] m_coord; } }
// Accessors.
size_t size() const { return m_size; }
float & x(size_t it) const { check_range(it); return m_coord[it*2 ]; }
float & x(size_t it) { check_range(it); return m_coord[it*2 ]; }
float & y(size_t it) const { check_range(it); return m_coord[it*2+1]; }
float & y(size_t it) { check_range(it); return m_coord[it*2+1]; }
private:
// Private helper.
void check_range(size_t it) const
{ if (it >= m_size) { throw std::out_of_range("Line index out of range"); } }
// Member data.
size_t m_size = 0; // number of points.
float * m_coord = nullptr; // memory buffer for the points.
}; /* end class Line */
/* Define the copy constructor */
Line::Line(Line const & other)
{
if (other.m_coord)
{
if (m_coord) { delete[] m_coord; } // free unused buffer.
m_coord = new float[other.m_size*2];
m_size = other.m_size;
std::copy_n(other.m_coord, other.m_size*2, m_coord);
}
else // the other object is empty.
{
if (m_coord)
{
delete[] m_coord; // free unused buffer.
m_coord = nullptr;
m_size = 0;
}
}
}
/* Define the move constructor */
Line::Line(Line && other)
{
std::swap(other.m_size, m_size);
std::swap(other.m_coord, m_coord);
}
/* Define the copy assignment operator */
Line & Line::operator=(Line const & other)
{
if (this == &other) { return *this; } // don't move to self.
// This part is the same as what's in the copy constructor.
if (other.m_coord)
{
if (m_coord) { delete[] m_coord; }
m_coord = new float[other.m_size*2];
m_size = other.m_size;
std::copy_n(other.m_coord, other.m_size*2, m_coord);
}
else
{
if (m_coord)
{
delete[] m_coord;
m_coord = nullptr;
m_size = 0;
}
}
return *this;
}
/* Define the move assignment operator */
Line & Line::operator=(Line && other)
{
if (this == &other) { return *this; } // don't move to self.
std::swap(other.m_size, m_size);
std::swap(other.m_coord, m_coord);
return *this;
}
int main(int, char **)
{
Line line(3);
line.x(0) = 0; line.y(0) = 1;
line.x(1) = 1; line.y(1) = 3;
line.x(2) = 2; line.y(2) = 5;
Line line2(line);
line2.x(0) = 9;
std::cout << "line: number of points = " << line.size() << std::endl;
for (size_t it=0; it<line.size(); ++it)
{
std::cout << "point " << it << ":"
<< " x = " << line.x(it)
<< " y = " << line.y(it) << std::endl;
}
std::cout << "line2: number of points = " << line.size() << std::endl;
for (size_t it=0; it<line.size(); ++it)
{
std::cout << "point " << it << ":"
<< " x = " << line2.x(it)
<< " y = " << line2.y(it) << std::endl;
}
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 9 10 | g++ constructor.cpp -o constructor --std=c++11
./constructor
line: number of points = 3
point 0: x = 0 y = 1
point 1: x = 1 y = 3
point 2: x = 2 y = 5
line2: number of points = 3
point 0: x = 9 y = 1
point 1: x = 1 y = 3
point 2: x = 2 y = 5
|
Rule of Five#
In C++ programming there are many coding guidance concluded by years of practice, and the rule of five is one of them. Originally it was the rule of three, stating that if any of the destructor, copy constructor, and copy assignment operator is customized, all of them should need to be customized.
Note
Default constructor, copy constructor, move constructor, copy assignment operator, move assignment operator, and destructor are the special member functions.
Modern C++ (C++11 and beyond) extends it to the rule of five, because of the addition of the move semantics. It becomes that if any of the following is implemented (does not use the implicit implementation), all of them should be explicitly implemented:
Destructor
Copy constructor
Copy assignment operator
Move constructor
Move assignment operator
When a class declaration is long, sometimes it is not obvious whether or not
the rule of five is followed. We can use the default keyword to always
write the special member functions even though we want to use the implicit
implementation.
1 2 3 4 5 6 7 8 9 10 | class Line
{
public:
Line() = default; // default constructor.
Line(Line const & ) = default; // copy constructor.
Line(Line &&) = default; // move constructor.
Line & operator=(Line const & ) = default; // copy assignment operator.
Line & operator=(Line &&) = default; // move assignment operator.
~Line() = default;
};
|
If there is not a custom implementation to a special member function, the
compiler generates an implicit one. But it is also possible to tell the
compiler to avoid the implicit implementation without providing the custom one.
It uses the delete keyword.
1 2 3 4 5 6 7 8 9 10 11 | class Line
{
public:
Line(double x0, double y0, double x1, double y1); // custom constructor.
Line() = delete; // remove the default constructor.
Line(Line const & ) = delete; // remove the copy constructor.
Line(Line &&) = delete; // remove the move constructor.
Line & operator=(Line const & ) = delete; // remove the copy assignment operator.
Line & operator=(Line &&) = delete; // remove the move assignment operator.
~Line() = default; // removing destructor doesn't make sense.
};
|
Note
Only the special member functions can be defaulted or deleted.
Standard Template Library (STL)#
Containers are essential to data processing. The STL provides efficient implementation of commonly used containers. They can be grouped in 3 categories:
Sequence containers:
std::vector,std::array,std::list,std::forward_list,std::deque.Associative containers:
std::map,std::set,std::multimap,std::multiset.Unordered associated containers:
std::unordered_map,std::unordered_set,std::unordered_multimap,std::unordered_multiset.
We will make a quick recapitulation for those we always use in numerical code:
std::vector, std::array, std::list, std::map, std::set,
std::unordered_map, std::unordered_set.
std::vector#
std::vector is one of the most useful STL containers. Whenever thinking of
using one-dimensional, variable-length arrays, we should consider whether or
not std::vector may be applicable.
std::vector#1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | #include <cstdint>
#include <stdexcept>
#include <vector>
#include <iostream>
int main(int, char **)
{
std::cout << "sizeof(std::vector<int>) = " << sizeof(std::vector<int>) << std::endl;
std::cout << "sizeof(std::vector<double>) = " << sizeof(std::vector<double>) << std::endl;
std::cout << "sizeof(std::vector<std::vector<double>>) = "
<< sizeof(std::vector<std::vector<double>>) << std::endl;
// Populate with an indexed loop.
std::vector<int> vec0;
for (size_t it=0; it<100; ++it) { vec0.push_back(it+1000); }
// Populate with iterators.
std::vector<int> vec1(vec0.begin()+20, vec0.begin()+25);
std::cout << "vec1 indices [20-25):" << std::endl;
for (int const v : vec1) { std::cout << " " << v << std::endl; }
try
{ vec1.at(10); } // Bound check.
catch (std::out_of_range e)
{ std::cout << "out of range exception: " << e.what() << std::endl; }
vec1.at(2) = 500;
vec1[3] = 600; // No bound check; dangerous.
std::cout << "vec1 modified:" << std::endl;
for (int const v : vec1) { std::cout << " " << v << std::endl; }
// The internal buffer may change from reallocation.
std::vector<int> data(10);
const int * ptr0 = data.data();
std::cout << "&data.at(0) = " << ptr0 << std::endl;
data.resize(100);
for (size_t it=0; it<10; ++it) { data.push_back(it+100); }
const int * ptr1 = data.data();
std::cout << "&data.at(0) = " << ptr1 << std::endl;
if (ptr0 != ptr1)
{
std::cout << "oops, address changes" << std::endl;
}
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | $ g++ vector.cpp -o vector --std=c++11
$ ./vector
sizeof(std::vector<int>) = 24
sizeof(std::vector<double>) = 24
sizeof(std::vector<std::vector<double>>) = 24
vec1 indices [20-25):
1020
1021
1022
1023
1024
out of range exception: vector
vec1 modified:
1020
1021
500
600
1024
&data.at(0) = 0x7fa868405c40
&data.at(0) = 0x7fa868406150
oops, address changes
|
std::array#
The class template array provides a type-safe alternate to C-style
fixed-size arrays.
std::array#1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | #include <cstdint>
#include <stdexcept>
#include <array>
#include <iostream>
int main(int, char **)
{
std::cout << "sizeof(std::array<int, 3>) = " << sizeof(std::array<int, 3>) << std::endl;
std::cout << "sizeof(std::array<int, 10>) = " << sizeof(std::array<int, 10>) << std::endl;
std::array<int, 3> arr1;
// Without bound check.
for (size_t it=0; it<arr1.size(); ++it)
{ arr1[it] = 100+it; }
// With bound check.
for (size_t it=0; it<arr1.size(); ++it)
{ arr1.at(it) = 100+it; }
std::cout << "arr1:" << std::endl;
for (int const v : arr1)
{ std::cout << " " << v << std::endl; }
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 | $ g++ array.cpp -o array --std=c++11
$ ./array
sizeof(std::array<int, 3>) = 12
sizeof(std::array<int, 10>) = 40
arr1:
100
101
102
|
std::list#
STL list supports constant time insertion and deletion of elements. Unlike
vector, iterators and references to an element in a list don’t get
invalidated by adding or removing other elements. list::splice supports
transferring of elements from one container to another without copy or
reallocation. The price to pay is the slower random access than vector.
std::list is usually implemented as a doubly-linked list.
std::list#1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | #include <cstdint>
#include <stdexcept>
#include <list>
#include <iostream>
int main(int, char **)
{
// Populate lst1.
std::list<int> lst1;
for (size_t it=0; it<3; ++it) { lst1.push_back(100+it); }
std::cout << "lst1:";
for (int v : lst1) { std::cout << " " << v; }
std::cout << std::endl;
// Populate lst2.
std::list<int> lst2;
for (size_t it=0; it<3; ++it) { lst2.push_front(200+it); }
std::cout << "lst2:";
for (int v : lst2) { std::cout << " " << v; }
std::cout << std::endl;
// Use an iterator to search for an element.
std::list<int>::iterator it;
for (it=lst2.begin(); it != lst2.end(); ++it)
{ if (*it == 201) { break; } }
// Erase the found element, and then insert a new one.
lst2.erase(it++);
lst2.insert(it, 301);
std::cout << "lst2 (modified):";
for (int v : lst2) { std::cout << " " << v; }
std::cout << std::endl;
// Transfer elements from lst1 to lst2 (splice).
lst2.splice(it, lst1, ++lst1.begin(), lst1.end());
std::cout << "lst1 (after splice):";
for (int v : lst1) { std::cout << " " << v; }
std::cout << std::endl;
std::cout << "lst2 (after splice):";
for (int v : lst2) { std::cout << " " << v; }
std::cout << std::endl;
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 | $ g++ list.cpp -o list --std=c++11
$ ./list
lst1: 100 101 102
lst2: 202 201 200
lst2 (modified): 202 301 200
lst1 (after splice): 100
lst2 (after splice): 202 301 101 102 200
|
std::map and std::set#
STL map is an ordered container for key-value pairs. The keys are unique
and don’t allow duplication. map is usually implemented as a red-black
tree. Search, insertion, and removal of elements in a map have logarithmic
time complexity.
STL set is a unique key container. Like map, it’s usually implemented
as a red-black tree.
std::map and std::set#1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | #include <cstdint>
#include <stdexcept>
#include <map>
#include <set>
#include <iostream>
int main(int, char **)
{
std::map<int, float> map1;
for (size_t it=5; it != 0; --it) { map1[it] = 1./float(it); }
std::cout << "map1:";
for (std::pair<int, float> const p : map1)
{ std::cout << " (" << p.first << "," << p.second << ")"; }
std::cout << std::endl;
std::cout << "map1 " << (map1.count(3) ? "has " : "does not have ")
<< "key 3" << std::endl;
std::cout << "map1 " << (map1.count(6) ? "has " : "does not have ")
<< "key 6" << std::endl;
std::set<int> set1;
for (size_t it=5; it != 0; --it) { set1.insert(it); }
std::cout << "set1:";
for (int const v : set1)
{ std::cout << " " << v; }
std::cout << std::endl;
std::cout << "set1 " << (set1.count(3) ? "has " : "does not have ")
<< "key 3" << std::endl;
std::cout << "set1 " << (set1.count(6) ? "has " : "does not have ")
<< "key 6" << std::endl;
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 | $ g++ map.cpp -o map --std=c++11
$ ./map
map1: (1,1) (2,0.5) (3,0.333333) (4,0.25) (5,0.2)
map1 has key 3
map1 does not have key 6
set1: 1 2 3 4 5
set1 has key 3
set1 does not have key 6
|
std::unordered_map and std::unordered_set#
STL unordered_map is also a container for key-value pairs. While the keys
are unique and don’t allow duplication, they do not have order.
unordered_map is usually implemented using hash table.
Search, insertion, and removal of elements in an unordered_map have
constant time complexity. On the other hand, those in a map have
logarithmic time complexity. While unordered_map usually offers faster
runtime than map, it tends to use more memory since red-black trees is very
efficient in memory usage.
Just like map having set, unordered_map also has a valueless
version called unordered_set. STL unordered_set, like
unordered_map, is usually implemented using hash table.
std::unordered_map and std::unordered_set#1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | #include <cstdint>
#include <stdexcept>
#include <unordered_map>
#include <unordered_set>
#include <iostream>
int main(int, char **)
{
std::unordered_map<int, float> map1;
for (size_t it=5; it != 0; --it) { map1[it] = 1./float(it); }
std::cout << "map1:";
for (std::pair<int, float> const p : map1)
{ std::cout << " (" << p.first << "," << p.second << ")"; }
std::cout << std::endl;
std::cout << "map1 " << (map1.count(3) ? "has " : "does not have ")
<< "key 3" << std::endl;
std::cout << "map1 " << (map1.count(6) ? "has " : "does not have ")
<< "key 6" << std::endl;
std::unordered_set<int> set1;
for (size_t it=5; it != 0; --it) { set1.insert(it); }
std::cout << "set1:";
for (int const v : set1)
{ std::cout << " " << v; }
std::cout << std::endl;
std::cout << "set1 " << (set1.count(3) ? "has " : "does not have ")
<< "key 3" << std::endl;
std::cout << "set1 " << (set1.count(6) ? "has " : "does not have ")
<< "key 6" << std::endl;
return 0;
}
|
Execution results:
1 2 3 4 5 6 7 8 | $ g++ unordered_map.cpp -o unordered_map --std=c++11
$ ./unordered_map
map1: (1,1) (2,0.5) (3,0.333333) (4,0.25) (5,0.2)
map1 has key 3
map1 does not have key 6
set1: 1 2 3 4 5
set1 has key 3
set1 does not have key 6
|
Polymorphism#
In C++, when a class has any member function that is virtual, it is polymorphic. C++ compiler knows the object is polymorphic, and uses the type information to find the associated member function in runtime.
To make the class Line polymorphic, we add an additional virtual function
length(), and make the destructor virtual too.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | class Line
{
public:
Line() = default;
Line(Line const & );
Line(Line &&);
Line & operator=(Line const & );
Line & operator=(Line &&);
Line(size_t size) : m_size(size), m_coord(new float[size*2]) {}
virtual ~Line() { if (nullptr != m_coord) { delete[] m_coord; } }
virtual float length() const;
size_t size() const { return m_size; }
float & x(size_t it) const { check_range(it); return m_coord[it*2 ]; }
float & x(size_t it) { check_range(it); return m_coord[it*2 ]; }
float & y(size_t it) const { check_range(it); return m_coord[it*2+1]; }
float & y(size_t it) { check_range(it); return m_coord[it*2+1]; }
private:
void check_range(size_t it) const
{ if (it >= m_size) { throw std::out_of_range("Line index out of range"); } }
size_t m_size = 0; // number of points.
float * m_coord = nullptr; // memory buffer for the points.
}; /* end class Line */
|
Then derive the class WeighedLine from it and override the virtual
functions:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | class WeighedLine : public Line
{
public:
WeighedLine(WeighedLine const & );
WeighedLine(WeighedLine &&);
WeighedLine & operator=(WeighedLine const & );
WeighedLine & operator=(WeighedLine &&);
WeighedLine(size_t size) : Line(size), m_weight(new float[size-1]) {}
virtual ~WeighedLine() override { delete[] m_weight; }
virtual float length() const override;
float const & weight(size_t it) const { return m_weight[it]; }
float & weight(size_t it) { return m_weight[it]; }
private:
float * m_weight = nullptr; // weight on line segments.
}; /* end class WeighedLine */
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 | #include <cstdint>
#include <algorithm>
#include <utility>
#include <cmath>
#include <iostream>
class Line
{
public:
Line() = default;
Line(Line const & );
Line(Line &&);
Line & operator=(Line const & );
Line & operator=(Line &&);
Line(size_t size) : m_size(size), m_coord(new float[size*2]) {}
virtual ~Line() { if (nullptr != m_coord) { delete[] m_coord; } }
virtual float length() const;
size_t size() const { return m_size; }
float & x(size_t it) const { check_range(it); return m_coord[it*2 ]; }
float & x(size_t it) { check_range(it); return m_coord[it*2 ]; }
float & y(size_t it) const { check_range(it); return m_coord[it*2+1]; }
float & y(size_t it) { check_range(it); return m_coord[it*2+1]; }
private:
void check_range(size_t it) const
{ if (it >= m_size) { throw std::out_of_range("Line index out of range"); } }
size_t m_size = 0; // number of points.
float * m_coord = nullptr; // memory buffer for the points.
}; /* end class Line */
/* Define the copy constructor */
Line::Line(Line const & other)
{
if (other.m_coord)
{
if (m_coord) { delete[] m_coord; } // free unused buffer.
m_coord = new float[other.m_size*2];
m_size = other.m_size;
std::copy_n(other.m_coord, other.m_size*2, m_coord);
}
else // the other object is empty.
{
if (m_coord)
{
delete[] m_coord; // free unused buffer.
m_coord = nullptr;
m_size = 0;
}
}
}
/* Define the move constructor */
Line::Line(Line && other)
{
std::swap(other.m_size, m_size);
std::swap(other.m_coord, m_coord);
}
/* Define the copy assignment operator */
Line & Line::operator=(Line const & other)
{
if (this == &other) { return *this; } // don't move to self.
// This part is the same as what's in the copy constructor.
if (other.m_coord)
{
if (m_coord) { delete[] m_coord; }
m_coord = new float[other.m_size*2];
m_size = other.m_size;
std::copy_n(other.m_coord, other.m_size*2, m_coord);
}
else
{
if (m_coord)
{
delete[] m_coord;
m_coord = nullptr;
m_size = 0;
}
}
return *this;
}
/* Define the move assignment operator */
Line & Line::operator=(Line && other)
{
if (this == &other) { return *this; } // don't move to self.
std::swap(other.m_size, m_size);
std::swap(other.m_coord, m_coord);
return *this;
}
float Line::length() const
{
float ret = 0;
for (size_t it=1; it<size(); ++it) {
ret += std::hypot(x(it) - x(it-1), y(it) - y(it-1));
}
return ret;
}
class WeighedLine : public Line
{
public:
WeighedLine(WeighedLine const & );
WeighedLine(WeighedLine &&);
WeighedLine & operator=(WeighedLine const & );
WeighedLine & operator=(WeighedLine &&);
WeighedLine(size_t size) : Line(size), m_weight(new float[size-1]) {}
virtual ~WeighedLine() override { delete[] m_weight; }
virtual float length() const override;
float const & weight(size_t it) const { return m_weight[it]; }
float & weight(size_t it) { return m_weight[it]; }
private:
float * m_weight = nullptr; // weight on line segments.
}; /* end class WeighedLine */
WeighedLine::WeighedLine(WeighedLine const & other)
: Line(other)
{
if (other.m_weight)
{
if (m_weight) { delete[] m_weight; } // free unused buffer.
m_weight = new float[other.size()-1];
std::copy_n(other.m_weight, other.size()-1, m_weight);
}
else // the other object is empty.
{
if (m_weight)
{
delete[] m_weight; // free unused buffer.
m_weight = nullptr;
}
}
}
WeighedLine::WeighedLine(WeighedLine && other)
: Line(other)
{
std::swap(other.m_weight, m_weight);
}
WeighedLine & WeighedLine::operator=(WeighedLine const & other)
{
if (this == &other) { return *this; }
Line::operator=(other);
if (other.m_weight)
{
if (m_weight) { delete[] m_weight; } // free unused buffer.
m_weight = new float[other.size()-1];
std::copy_n(other.m_weight, other.size()-1, m_weight);
}
else // the other object is empty.
{
if (m_weight)
{
delete[] m_weight; // free unused buffer.
m_weight = nullptr;
}
}
return *this;
}
WeighedLine & WeighedLine::operator=(WeighedLine && other)
{
if (this == &other) { return *this; }
Line::operator=(other);
std::swap(other.m_weight, m_weight);
return *this;
}
float WeighedLine::length() const
{
float ret = 0;
for (size_t it=1; it<size(); ++it) {
ret += weight(it-1) * std::hypot(x(it) - x(it-1), y(it) - y(it-1));
}
return ret;
}
int main(int, char **)
{
std::cout << "sizeof(Line) = " << sizeof(Line) << std::endl;
std::cout << "sizeof(WeighedLine) = " << sizeof(WeighedLine) << std::endl;
WeighedLine line(3);
line.x(0) = 0; line.y(0) = 1;
line.x(1) = 5; line.y(1) = 1; line.weight(0) = 1;
line.x(2) = 5; line.y(2) = 4; line.weight(1) = 2;
Line line2(line);
line2.x(0) = 2;
WeighedLine * pwline3 = new WeighedLine(line);
Line * pline3 = pwline3;
// Without runtime information the compiler cannot know whether or not downcasting is safe.
// error: assigning to 'WeighedLine *' from incompatible type 'Line *'
//pwline3 = pline3;
// RTTI knows pline3 points to a WeighedLine object, so this downcasting is fine.
pwline3 = dynamic_cast<WeighedLine *>(pline3);
std::cout << "downcasting from Line * to WeighedLine * works on a WeighedLine object: pwline3= " << pwline3 << std::endl;
WeighedLine * pwline2;
pwline2 = dynamic_cast<WeighedLine *>(&line2);
std::cout << "downcasting from Line * to WeighedLine * fails on a Line object: pwline2 = " << pwline2 << std::endl;
pwline3->x(0) = 3;
std::cout << "Object type of pwline3: " << typeid(*pwline3).name() << std::endl;
std::cout << "Object type of pline3: " << typeid(*pline3).name() << std::endl;
std::cout << "line: number of points = " << line.size() << std::endl;
for (size_t it=0; it<line.size(); ++it)
{
std::cout << "point " << it << ":"
<< " x = " << line.x(it)
<< " y = " << line.y(it);
if (it != 0)
{
std::cout << " weight = " << line.weight(it-1);
}
std::cout << std::endl;
}
std::cout << " length = " << line.length() << std::endl;
std::cout << "line2: number of points = " << line.size() << std::endl;
for (size_t it=0; it<line.size(); ++it)
{
std::cout << "point " << it << ":"
<< " x = " << line2.x(it)
<< " y = " << line2.y(it);
// This doesn't build.
/*if (it != 0)
{
// error: no member named 'weight' in 'Line'
std::cout << " weight = " << line2.weight(it-1);
}*/
std::cout << std::endl;
}
std::cout << " length = " << line2.length() << std::endl;
Line & line3 = *pline3;
std::cout << "line3: number of points = " << line3.size() << std::endl;
for (size_t it=0; it<line3.size(); ++it)
{
std::cout << "point " << it << ":"
<< " x = " << line3.x(it)
<< " y = " << line3.y(it);
// This doesn't build.
/*if (it != 0)
{
std::cout << " weight = " << line3.weight(it-1);
}*/
std::cout << std::endl;
}
std::cout << " length = " << line3.length() << std::endl;
WeighedLine & wline3 = *pwline3;
std::cout << "wline3: number of points = " << wline3.size() << std::endl;
for (size_t it=0; it<wline3.size(); ++it)
{
std::cout << "point " << it << ":"
<< " x = " << wline3.x(it)
<< " y = " << wline3.y(it);
if (it != 0)
{
std::cout << " weight = " << wline3.weight(it-1);
}
std::cout << std::endl;
}
std::cout << " length = " << wline3.length() << std::endl;
delete pline3;
return 0;
}
|
To make the polymorphism work correctly, the derived class also needs to implement the copy and move constructors and assignment operators by taking the base class into account.
With the example we will observe the following things:
When the derived class needs addition data, the memory management becomes much more complex.
A pointer to the base class can point to a derived object. (Up-casting is fine.)
A pointer to the derived class can NOT point to a base object. (Down-casting is forbidden by default.)
To downcast polymorphic objects, you need to use
dynamic_castto let RTTI (run-time type information) do the work.RTTI makes the object know the correct virtual function to call. Although
line3is declared as reference to the base class (Line &),WeighedLine::length()is called.
Execution results:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | $ g++ polymorphic.cpp -o polymorphic --std=c++11
$ ./polymorphic
sizeof(Line) = 24
sizeof(WeighedLine) = 32
downcasting from Line * to WeighedLine * works on a WeighedLine object: pwline3= 0x7fda8dc05b00
downcasting from Line * to WeighedLine * fails on a Line object: pwline2 = 0x0
Object type of pwline3: 11WeighedLine
Object type of pline3: 11WeighedLine
line: number of points = 3
point 0: x = 0 y = 1
point 1: x = 5 y = 1 weight = 1
point 2: x = 5 y = 4 weight = 2
length = 11
line2: number of points = 3
point 0: x = 2 y = 1
point 1: x = 5 y = 1
point 2: x = 5 y = 4
length = 6
line3: number of points = 3
point 0: x = 3 y = 1
point 1: x = 5 y = 1
point 2: x = 5 y = 4
length = 8
wline3: number of points = 3
point 0: x = 3 y = 1
point 1: x = 5 y = 1 weight = 1
point 2: x = 5 y = 4 weight = 2
length = 8
|
Polymorphism incurs runtime penalty. It is OK in two scenarios:
Runtime work is unavoidable. We trust the compiler does a better job than writing branching code ourselves.
Timing doesn’t matter. When the code isn’t in the inner loop of computation, inefficiency may be negligible.
As we see, to make polymorphism work, there is a lot of code to write. Therefore in high-performance numerical code we use polymorphism with great caution.
Curiously Recursive Template Pattern (CRTP)#
If we want to make a class hierarchy polymorphic without the runtime overhead, CRTP helps. Usually the word polymorphism means dynamic polymorphism, as we described in the previous section. If the classes behave as polymorphic but all the type information is determined during compile time, it is called static polymorphism.
Static polymorphism has two major benefits (at the cost of being limited in compile time). First is to not have runtime overhead. The second is to avoid the memory overhead associated with virtual functions. RTTI needs some information to determine types in runtime. That is usually (if not always) accomplished by a virtual function table, which at least add one more word on every polymorphic object. For very small objects, like a resource handle, which usually occupies one or two words, it’s a great overhead.
This is how a CRTP hierarchy looks like. PointBase is our class template
base. CartesianPoint and PolarPoint pass themselves into the base
class’ template argument, so PointBase can see and access the derived
classes’ function to provide a common interface.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | template <class Derived>
class PointBase
{
public:
constexpr static const double PI = 3.14159265358979323846;
PointBase(float v0, float v1) : m_v0(v0), m_v1(v1) {}
float const & v0() const { return m_v0; }
float & v0() { return m_v0; }
float const & v1() const { return m_v1; }
float & v1() { return m_v1; }
float dist() const
{
// Prevent the derived class from working if it doesn't define dist(),
// just like what a pure virtual function does.
static_assert(&PointBase<Derived>::dist != &Derived::dist,
"derived class must define dist()");
return derived().dist();
}
private:
Derived const & derived() const { return *static_cast<Derived const *>(this); }
float m_v0, m_v1;
}; /* end class PointBase */
class CartesianPoint : public PointBase<CartesianPoint>
{
public:
using base_type = PointBase<CartesianPoint>;
using base_type::base_type;
float dist() const
{
return std::hypot(v0(), v1());
}
}; /* end class CartesianPoint */
class PolarPoint : public PointBase<PolarPoint>
{
public:
using base_type = PointBase<PolarPoint>;
using base_type::base_type;
float dist() const
{
return std::abs(v0());
}
}; /* end class PolarPoint */
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 | #include <cstdint>
#include <algorithm>
#include <utility>
#include <cmath>
#include <iostream>
template <class Derived>
class PointBase
{
public:
constexpr static const double PI = 3.14159265358979323846;
PointBase(float v0, float v1) : m_v0(v0), m_v1(v1) {}
float const & v0() const { return m_v0; }
float & v0() { return m_v0; }
float const & v1() const { return m_v1; }
float & v1() { return m_v1; }
float dist() const
{
// Prevent the derived class from working if it doesn't define dist(),
// just like what a pure virtual function does.
static_assert(&PointBase<Derived>::dist != &Derived::dist,
"derived class must define dist()");
return derived().dist();
}
private:
Derived const & derived() const { return *static_cast<Derived const *>(this); }
float m_v0, m_v1;
}; /* end class PointBase */
class CartesianPoint : public PointBase<CartesianPoint>
{
public:
using base_type = PointBase<CartesianPoint>;
using base_type::base_type;
float dist() const
{
return std::hypot(v0(), v1());
}
}; /* end class CartesianPoint */
class PolarPoint : public PointBase<PolarPoint>
{
public:
using base_type = PointBase<PolarPoint>;
using base_type::base_type;
float dist() const
{
return std::abs(v0());
}
}; /* end class PolarPoint */
class BadPoint : public PointBase<BadPoint>
{
public:
using base_type = PointBase<BadPoint>;
using base_type::base_type;
// Intentionally omit dist().
/*float dist() const
{
return 0.0;
}*/
}; /* end class BadPoint */
int main(int, char **)
{
std::cout << "sizeof(CartesianPoint) = " << sizeof(CartesianPoint) << std::endl;
std::cout << "sizeof(PolarPoint) = " << sizeof(PolarPoint) << std::endl;
CartesianPoint cpt(1, 1);
PolarPoint ppt(1, PolarPoint::PI / 4);
std::cout << "CartesianPoint(1,1)::dist() = " << cpt.dist() << std::endl;
std::cout << "PolarPoint(1, pi/4)::dist() = " << ppt.dist() << std::endl;
// This doesn't build.
// error: static_assert failed "derived class must define dist()"
//std::cout << "BadPoint(1, 1)::dist() = " << BadPoint(1,1).dist() << std::endl;
return 0;
}
|
Execution results:
1 2 3 4 5 6 | $ g++ crtp.cpp -o crtp --std=c++11
$ ./crtp
sizeof(CartesianPoint) = 8
sizeof(PolarPoint) = 8
CartesianPoint(1,1)::dist() = 1.41421
PolarPoint(1, pi/4)::dist() = 1
|
Exercises#
In array.cpp, what may happen if you write the following code?
data[-1] = 0;
Given 2 single-precision floating-point values, 0.3 and -0.3. Reinterpret (not integer to floating-point casting) their data (bits) as 32-bit unsigned integers. What is the integer value after performing XOR of the two integers? Change the floating-point values to 183.2 and -183.2. What is the value after XOR again?
What are the member data (including types) in the
std::vectorimplementation in the STL in the compiler you use?Reimplement the class
Lineby using STL containers instead of raw pointers (do not copy-n-paste the following code listing):1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
class Line { public: Line(); Line(Line const & ); Line(Line &&); Line & operator=(Line const & ); Line & operator=(Line &&); Line(size_t size); ~Line(); size_t size() const; float & x(size_t it) const; float & x(size_t it); float & y(size_t it) const; float & y(size_t it); private: // Member data. }; /* end class Line */ int main(int, char **) { Line line(3); line.x(0) = 0; line.y(0) = 1; line.x(1) = 1; line.y(1) = 3; line.x(2) = 2; line.y(2) = 5; Line line2(line); line2.x(0) = 9; std::cout << "line: number of points = " << line.size() << std::endl; for (size_t it=0; it<line.size(); ++it) { std::cout << "point " << it << ":" << " x = " << line.x(it) << " y = " << line.y(it) << std::endl; } std::cout << "line2: number of points = " << line.size() << std::endl; for (size_t it=0; it<line.size(); ++it) { std::cout << "point " << it << ":" << " x = " << line2.x(it) << " y = " << line2.y(it) << std::endl; } return 0; }